Talk by Prof. Dr. Patrick Jenny (ETH Zurich)
We are pleased to invite you to a special research talk. Prof. Dr. Patrick Jenny from ETH Zurich will present a recent contribution from his ongoing research as part of our lecture series.
Title of the Talk:
“Data Driven Corrections of Turbulent Flow Simulations and Modeling”
Date: 18 December 2025
Time: 15:00
Location: ZEI, Building 5414, Lichtenbergstraße 4a, Garching, Room 002
We warmly welcome all interested participants and look forward to your attendance!
Abstract:
Accurate simulation of turbulent flows remains a challenge due to the high computational cost of direct numerical simulations (DNS) and the limitations of traditional turbulence models. This talk is divided into two parts; both coping with deficiencies of existing turbulence models trying to compensate for errors based on sparse empirical data.
Part I deals with 4D (space and time) variational data assimilation (4DvarDA). While variational data assimilation (DA) has proven very successful in assimilating sparse reference data to improve numerical predictions of steady averaged turbulent flow fields, it generally becomes computationally extremely expensive for unsteady flow problems. To cope with the cost of variational DA for unsteady flows, we developed a 3D variational DA framework that incorporates a time-discrete Fourier transform of the unsteady Reynolds averaged Navier-Stokes (URANS) equations, facilitating the use of the stationary discrete adjoint method in Fourier space.
Central to our methodology is the introduction of a corrective, divergence-free, and unsteady forcing term (correction of the modeled Reynolds force), derived from a Fourier series expansion, into the URANS equations. This term aims at mitigating discrepancies in the modeled divergence of Reynolds stresses, allowing for the tuning of stationary parameters across different Fourier modes. While designed to accommodate multiple modes in general, the basic capabilities of the framework are demonstrated for a setup that is truncated after the first Fourier mode. The effectiveness of the approach is demonstrated through its application to turbulent flow around a two dimensional circular cylinder at a Reynolds number of 3900. Our results highlight the method’s ability to reconstruct mean flow accurately and improve the vortex shedding frequency (Strouhal number) through the assimilation of zeroth mode data. Additionally, the assimilation of first mode data further enhances the simulation’s capability to capture low-frequency dynamics of the flow, and finally, it runs efficiently by leveraging a coarse mesh. It also is shown shown that this approach is promising for assimilation data to improve large eddy simulations (LES) results.
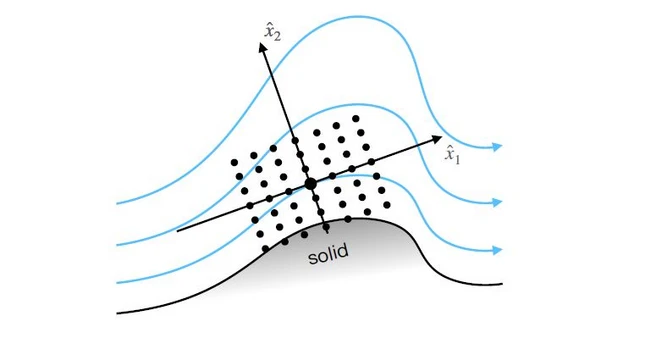
In Part II, Non-Linear Super-Stencils (NLSS) to augment standard models for RANS simulations are presented and discussed. The method introduces a fully connected neural network that learns a mapping from the local mean flow field to a corrective (Reynolds) force term, which is added to a standard RANS solver in order to align its solution with high-fidelity data; an illustration of an NLSS is shown in Fig. 1. A procedure is devised to extract training data from reference DNS and LES.
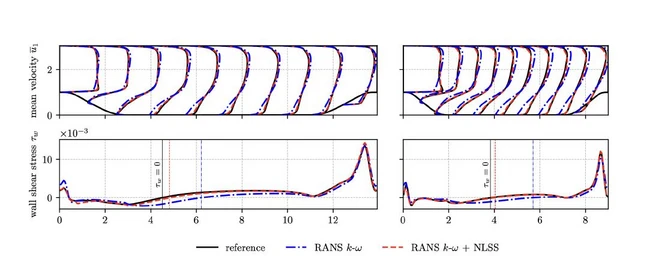
To reduce the complexity of the non-linear mapping, the dimensionless local flow data is aligned with the local mean velocity, and the local support domain is scaled by the turbulent integral length scale. After being trained on a single periodic hill case, the NLSS-corrected RANS solver is shown to generalize to different periodic hill geometries and different Reynolds numbers, producing significantly more accurate solutions than the uncorrected RANS simulations. For demonstration, Fig. 2 shows RANS simulation results with and without NLSS-correction along with high fidelity references (mean velocity profiles in the top plots and wall shear stresses on the bottom) of two test cases which were not used for training. For training a domain of lenth L = 9m, a hill stretch factor of = 1 and a Reynolds number of Re = 10595 were considered, while L = 13:929m, = 1:5 and Re = 5600 were chosen for the left test case and L = 9m, = 1 and Re = 19000 for right test case.
For both test cases it can be observed that the NLSS-corrected RANS solutions closely agree with the reference data (much better than the uncorrected ones), thus demonstrating the ability of the NLSS to generalize across different geometries and Reynolds numbers. While the ability of NLSS for model correction is demonstrated here for turbulent flows, the concept is more general and will be explored in the future for other systems of partial differential equations involving physical models.
Jonas Luther, Justin Plogmann, Oliver Brenner, Patrick Jenny - Swiss Federal Institute of Technology (ETH), Zürich, Switzerland