Zum Inhalt springen
Technische Universität München

Adaptive Levelset PArallel Code ALPACA

General classification

Programming 
language

Code
architectures

Adaptive mesh
finite volume simulations

In diverse engineering applications, compressible single- and multi-phase flow scenarios manifest, featuring, for example, straight and oblique shocks in nozzle flows, resulting in abrupt fluid state changes. Similarly, high-velocity impacts of liquid drops on rigid and elastic surfaces generate pressure waves that lead to drop explosion. In cavitation, vapor or gas bubbles collapse, inducing ultra-fast jets and high-pressure loads on nearby walls, vital in surface cleaning, surface erosion, and kidney stone destruction. We have pioneered the advanced flow solver ALPACA in the past decade, robustly addressing multi-scale compressible single- and multi-phase flows. Key features of the flow solver are vanishing artificial smearing of flow states, non-oscillatory treatment of discontinuities (e.g., shocks), and the enforcement of discrete conservation. Our tool enables precise numerical assessments, contributing to a deeper understanding of these intricate fluid dynamics with potential implications of diverse applications. ALPACA is optimized for large scale simulations on CPUs and is entirely written in C++ with a minimal inclusion of third-party libraries. Currently, we are working to integrate ALPACA also for acceleration units such as GPUs to further improve the flexibility and performance of the code framework.

Modularity concept

Modularity concept of ALPACA.

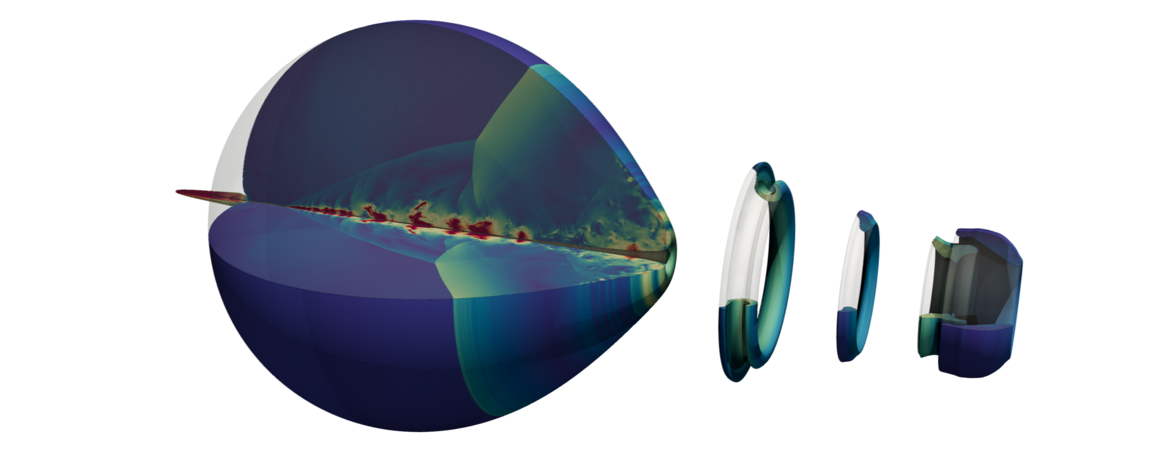
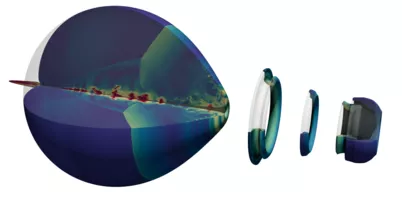
ALPACA is an Eulerian multi-phase code framework that solves the compressible Navier-Stokes equations with a flux-based finite-volume discretization. This capability empowers the simulation of high-velocity flows, including the formation of flow discontinuities. The emergence of discontinuities is resolved with robust Riemann solvers and high-order reconstruction stencils. A key feature of ALPACA is its modular design, providing maximum flexibility tailored to the specific demands of a given application. Moreover, the Cartesian Eulerian mesh continuously adapts to the evolving flow using a wavelet-based refinement strategy. This design ensures computational efficiency across diverse and complex multi-scale flow scenarios without a priori knowledge about the flow. To enrich the fidelity of the simulation in capturing underresolved structures, ALPACA incorporates a two-way coupled Lagrangian particle solver.

Multi-phase flow simulations

Aerobreakup simulation of a shock with speed Ma = 2.4 passing over a water droplet for different multi-phase model: diffuse-interface Γ-model (left) and sharp-interface levelset method (right).

A pivotal feature of ALPACA lies in its capability to simulate high-resolution compressible multi-phase flows. Therefore, we provide a variety of state-of-the-art interface treatments, encompassing sharp- to diffuse-interface methods, such as level-set, DEM, and Γ-model. The comparison on the right illustrates the efficacy of both sharp- (right frame) and diffuse-interface methods (left frame) in accurately reproducing macroscopic experimental results of an aero-breakup scenario involving the impact of a planar shock on a gas bubble. However, the Γ-model, characterized by its diffusivity, introduces distinctive interface deformations and wake structures compared to the sharp-interface level-set method, where the interaction of shock-waves with the interface is always resolved accurately. This precision stems from the inherent separation of the different fluid components within the model.

The different multi-phase treatments in ALPACA not only ensure maximum flexibility but also provide high-accuracy models where each multi-phase model has its own essential characteristics. The sharp-interface level-set method has the highest interface fidelity and imposes minimal restrictions on the underlying material equation of state. However, these advantages come with increased methodological complexity, higher memory consumption, and performance drawbacks. Conversely, diffuse-interface methods offer a more straightforward adaptation for multi-component simulations. 

Comparison of numerical complexity, interfacial accuracy, and computational efficiency of different multi-phase models implemented in ALPACA.

Machine learning and meta data integration

Schematic representation of embedding ALPACA in open- and closed-loop applications including meta-data generation.

We contribute to the rapidly expanding field of machine learning for engineering systems by integrating ALPACA as a closed-loop application for adaptive experimentation. The simulation process involves three main steps: pre-processing, simulation execution, and post-processing. During pre-processing, adjustments are made to the code framework to accommodate varying user specifications, ensuring ALPACA is compiled appropriately, and input settings for the simulation run. Following simulation execution, the post-processor analyzes quantities of interest (QoIs) for further investigation. Upon obtaining QoIs, the system can operate in either an open-loop or closed-loop scenario. In the open-loop framework, single or multiple simulation runs generate datasets suitable for machine learning applications such as Gaussian processes or neural networks. These datasets can also be utilized for community-wide data sharing and collaboration. Alternatively, in the closed-loop paradigm, QoIs serve as inputs for Bayesian optimization or reinforcement learning algorithms, guiding the initiation of new simulation executions with adjusted initial conditions. This iterative process enhances the efficiency and effectiveness of the simulation-based experimentation approach, enabling adaptive decision-making and optimization in engineering systems.

An essential aspect for dataset generation, open-loop analysis, or closed-loop applications is accurate management of code metadata, encompassing compiler settings, module versioning, investigated scenarios, and user specifications configured at compile time. Ensuring a comprehensive understanding of code metadata is vital for reproducibility across various scenarios and simulation campaigns. Within ALPACA, we accurately capture and provide a comprehensive set of metadata for each simulation run, documenting all chosen settings. Moreover, we maintain a dynamic relationship with researchers from NFD4Ing, ensuring our metadata remains aligned with the latest state-of-the-art requirements and the rapid evolution of new engineering ontologies. This collaborative effort guarantees that our metadata infrastructure is continuously updated to meet the dynamic needs of the engineering research community, facilitating robust reproducibility and effective utilization of simulation data.

Applications

Shock-dominated 
flows

Complex wave
interactions

Multi-phase
flows

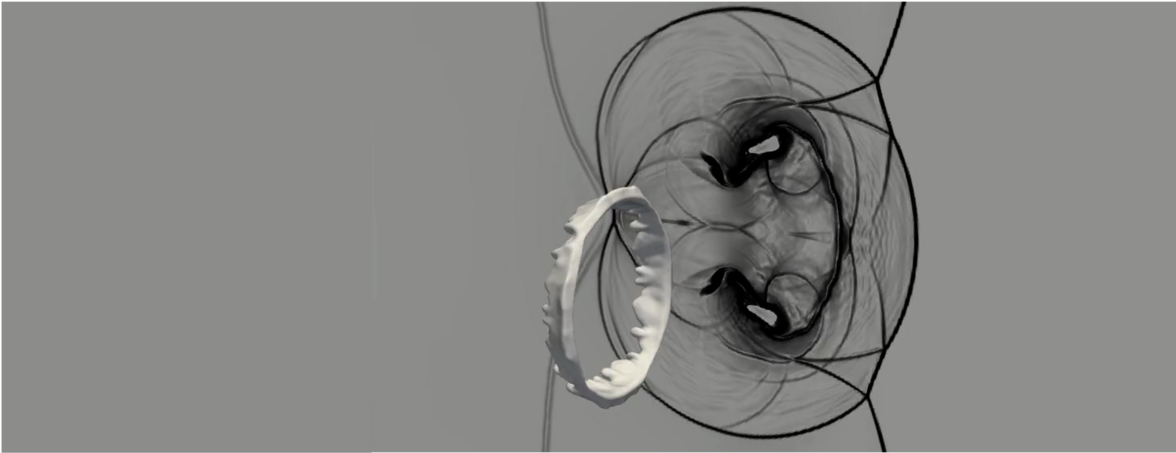
ALPACA serves as a versatile tool to simulate complex multi-scale flows, including strong shocks, complex wave patterns, and turbulent flows. The effectiveness of the multi-phase models is exemplified in their successful application to simulate diverse phenomena, ranging from dendrite growth, free-surface flows, and cavitating flows. In latter, the combination of the flow solver with the Lagrangian particle solver allows, for example, to investigate particle surface cleaning mechanism achieved through the interaction of multiple simultaneously generated laser-induced cavitation bubbles. Strong shear flow, induced by ultra-fast jets during the collapse phase of the bubbles, enables particle cleaning. The sharp-interface level-set method further extends the numerical investigation of single- and multi-phase flows near complex boundaries. For exmaple the flow in a high-velocity oxygen fuel gun (HVOF) featuring multiple fluid inlets has been simulated successfully.

Multi-phase flows

In ALAPCA distinct multi-phase models are implemented, ranging from a sharp-interface level-set method towards diffuse Γ-model and DEM. The levelset method maintains a sharp interface throughout the simulation and prevents artificial smearing/mixing across the interface, while the Γ-model allows artificial mixing in a narrow region around the interface. In DEM a mixed approach is considered, where all phases are treated separately and interaction terms are imposed explicitly at the interface.

Shock-induced collapse (gas bubble within liquid)

      Γ-model                                                                                             Levelset method

Shock-induced collapsed (liquid drop within gas)

      Γ-model                                                                                             Levelset method

Shock-induced collapse (R22-Helium gas bubble in air) simulated with DEM

Laser-induced cavitation

ALAPCA has been successfully employed to simulate laser-induced cavitation, including single bubbles near a planar solid wall at various standoff distances, multiple bubble interactions in the free field, and the collapse of multiple bubbles near a planar wall inducing particle surface cleaning. In these scenarios, high-speed supersonic jets can form, which are accurately captured by ALAPCA's high-order numerical schemes. These simulations require large domains to ensure the correct pressure field surrounding the bubbles (L/R = 100). ALAPCA addresses these challenges with adaptive mesh refinement techniques, enabling strong mesh compression in the region of interest and significant mesh coarsening towards the domain boundaries.

Single bubble dynamics near planar solid wall

    Standoff distance 0.1                                          Standoff distance 0.5                                           Standoff distance 1.0

Double bubble free-field at standoff distance 0.76

Particle surface cleaning by multiple bubbles

Free surface flows

We use the sharp-interface level-set method in ALAPCA to simulate free-surface flows, focusing on wave dynamics in the heavy fluid phase on one side of the interface. For the lighter fluid on the other side, we impose a fixed pressure boundary to avoid costly computations. ALAPCA's adaptive mesh refinement technique ensures high-resolution moving interface dynamics while coarsening the entire light fluid phase, optimizing computational efficiency.

Deep Splash We = 358

Crown splash We = 2010

Complex geometry flows

In ALAPCA, we use the sharp-interface level-set method to simulate complex boundary flows, currently supporting static (non-moving) boundaries. ALAPCA's adaptive mesh refinement technique enables mesh refinement near the boundary while applying coarser resolutions within the fluid phase. Thanks to ALAPCA's block structure, we can eliminate computations in the solid phase entirely, ensuring high-performance simulations.

Nozzle flow for HVOF spray guns

Solidification

The level-set method can also be applied to impose a dynamic boundary due to the sharp separation of two phases. We have successfully used this technique to simulate the evolution of the solidification front in dendritic growth scenarios. The level-set evolution is solved semi-implicitly, enabling the use of interface dynamics to compute the interface boundary condition accurately.

Dendritic growth

Publications

To top